請問一題數學題,不知怎麼解釋給小孩懂..

referee_c

*停權中*

加入日期: Aug 2005

文章: 279

引用:

作者Crazynut

哥哥跑了幾公尺，弟弟跑了幾公尺……這種表示方式總令我想起古希臘有名的謬論。

萬一小孩子天賦異秉推導出，"哥哥永遠追不上弟弟"的結論就很不妙了……

我個人很不喜歡這種解釋法，所以我寧願用代數。

弟弟領先的時間不是無限大,會收斂在某個值.

不過這個問題,高中數學才會用極限去解釋.

2014-08-15, 10:42 AM #31

Crazynut

Master Member

加入日期: Apr 2001

您的住址: 高雄

文章: 2,247

引用:

作者referee_c

弟弟領先的時間不是無限大,會收斂在某個值.

不過這個問題,高中數學才會用極限去解釋.

當然這必須以極限和連續的觀念來解釋。

但是當你以"哥哥跑了幾公尺，弟弟跑了幾公尺"來解題時，就已經無意中將時間切段了，它不是連續的。將它放大時問題還不會顯露，但縮小時就會出現追不上烏龜的障壁……

而且最頭痛的是，它在邏輯上是完全沒有問題的，所以才困擾了古希臘人這麼久。

所以我才說這種解法不好，觀念上有問題、有瑕疪。

__________________
簽名檔真是礙眼…還是讓版面乾淨點吧！

2014-08-15, 11:16 AM #33

Adsmt

Golden Member

加入日期: Feb 2004

您的住址: 從來處來

文章: 2,762

引用:

作者Crazynut

當然這必須以極限和連續的觀念來解釋。
但是當你以"哥哥跑了幾公尺，弟弟跑了幾公尺"來解題時，就已經無意中將時間切段了，它不是連續的。將它放大時問題還不會顯露，但縮小時就會出現追不上烏龜的障壁……
而且最頭痛的是，它在邏輯上是完全沒有問題的，所以才困擾了古希臘人這麼久。
所以我才說這種解法不好，觀念上有問題、有瑕疪。

事情沒你說的這麼嚴肅，也沒這麼困擾；

http://zh.wikipedia.org/wiki/%E8%8A...%82%96%E8%AB%96
如柏拉圖描述，芝諾說這樣的悖論，是興之所至的小玩笑。首先，巴門尼德編出這個悖論，用來嘲笑「數學派」所代表的畢達哥拉斯的「1>0.999..., 1-0.999...>0」思想。然後，他又用這個悖論，嘲笑他的學生芝諾的「1=0.999..., 但1-0.999...>0」思想。最後，芝諾用這個悖論，反過來嘲笑巴門尼德的「1-0.999...=0, 或1-0.999...>0」思想。

2014-08-15, 12:22 PM #35

Hoyagi Senior Member 加入日期: Aug 2001 您的住址: 台北文章: 1,012	謝謝大家的指導,中午已講解二種解法給兒子聽了,說是了解了..其他就看他自已理解力了.. 因為他今年小四升小五,只是先教他先修國小到小六的數學課程...先懂個八.九成即可..
2014-08-15, 01:27 PM #36

LALALOVE

Regular Member

加入日期: Apr 2007

文章: 54

引用:

作者Hoyagi

因功力不夠,但不想小孩讀死書,所以數學題我都盡量要求他解題時,了解"為什麼"這樣算,但小弟功力太爛,只好上網求助了

評量的解答如下..我試著解釋看看評量解答的想法如下

250÷(3.5－1)＝100
100×3.5＝350

答：哥哥跑350公尺，弟弟跑100公尺

..小弟試著解釋解題式子的想法..
250÷(3.5－1)＝100 <因哥速度是弟的3.5倍,所以弟每跑1公尺哥哥跑3.5公尺,而一啟跑哥等於先讓弟一圈250M開始追,因弟每跑1公尺,哥可追"近"2.5公尺,在相差250公尺的狀況下,哥要追上弟等於弟跑100"個"公尺時

100×3.5＝350
弟跑100公尺,哥是弟的3.5倍,所以哥就是弟跑的距離X3.5=350公尺

答：哥哥跑350公尺，弟弟跑100公尺

------------------------------------------------------------------------
我的另一個想法是(250+X)/3.5=X

X代表弟弟跑了几公尺會被追上,那...

依照樓主所提供的評量解答來看，這應該是小六下學期「基準量和比較量」這個單元的題目

但首先你要先跟小朋友解釋下面兩個觀念

第一，當哥哥追上弟弟時，哥哥會比弟弟多跑一圈，也就是多跑了250公尺（如下圖）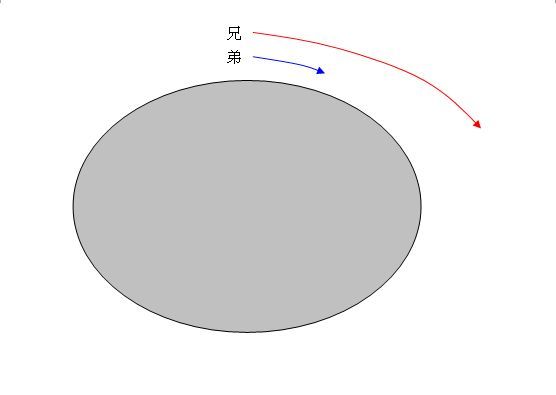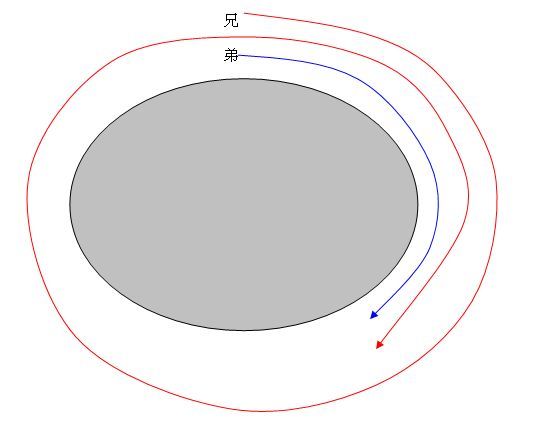

第二，由於兩人同時出發，所以當哥哥追上弟弟時，兩人所花的時間相同，但哥哥的速度是弟弟的3.5倍，所以哥哥跑的距離也會是弟弟的3.5倍

接下來，你就可以依照「基準量和比較量」這個單元的方法解釋給他聽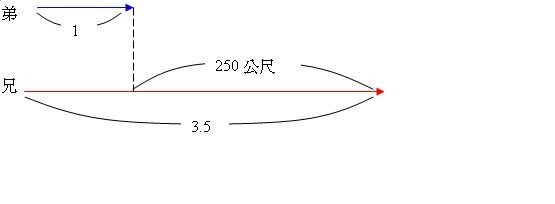

把弟弟跑的距離當成1倍，哥哥跑的距離當成3.5倍，哥哥比弟弟多跑了250公尺，而這250公尺恰為弟弟的2.5倍

接下來的算式就和評量一樣

250÷(3.5－1)＝100
100×3.5＝350

答：哥哥跑350公尺，弟弟跑100公尺

如果您的小朋友對「基準量和比較量」的觀念不熟，或是還沒學到這個單元

你可以先看看國小數學第12冊的課本相關內容

部編版的線上版在下面的網址（在2-2和2-3的部份）
http://wd.naer.edu.tw/102-12/10212-2.htm

__________________
想念.....

2014-08-15, 01:31 PM #37

Hoyagi Senior Member 加入日期: Aug 2001 您的住址: 台北文章: 1,012	謝謝你的圖表說明太讚了....下午我兒子回來我會叫他上來看這解答...感謝 [QUOTE=LALALOVE]依照樓主所提供的評量解答來看，這應該是小六下學期「基準量和比較量」這個單元的題目
2014-08-15, 01:40 PM #38

Mschumacher

Major Member

加入日期: Mar 2002

您的住址: de_dust2@Taipei

文章: 184

引用:

作者referee_c

引用:

作者Mschumacher

這讓我想到小學的時候老師問了一個全班只有兩個人答對的問題
有三支錶哪一支錶比較準
1. 一天準時兩次
2. 一星期準時一次
3. 一年準時一次
1.壞了.
2.一星期就慢或快12小時.
3.一年才快或慢12小時.

恩當初全班4X人只有兩個人選3
剩下的人裡面 1/3選1 2/3選2 XD

__________________
沒辦法家裡窮~

2014-08-15, 02:03 PM #39

在.遇見你的地方 Basic Member 加入日期: Apr 2010 文章: 11	偷偷路過哥哥需跑完一圈+再加上弟弟跑的部份=兩人相遇的地方 250+x=3.5x 2.5X=250 x=100 3.5x=350
2014-08-15, 11:31 AM #34

212412 停權中加入日期: Jan 2013 您的住址: 府城文章: 9	哥哥:操場有250公尺的? 弟弟:爸爸跑到哪裡去了? 媽媽: 你爸跑在年輕辣妹後面....
2014-08-15, 02:04 PM #40